У другій частині ми розглянемо популярний алгоритм RSA, де при шифруванні використовується публічний ключ. Але спочатку хочу попередити вас ще раз. Код, представлений в цій статті, призначений тільки для ознайомлювальних цілей. Криптографія - дуже велика і складна область, і щоб у вас не було проблем, я не рекомендую шифрувати інформацію за допомогою моєї вироби.

Автор: Malarkey

У другій частині ми розглянемо популярний алгоритм RSA, де при шифруванні використовується публічний ключ. Але спочатку хочу попередити вас ще раз. Код, представлений в цій статті, призначений тільки для ознайомлювальних цілей. Криптографія - дуже велика і складна область, і щоб у вас не було проблем, я не рекомендую шифрувати інформацію за допомогою моєї вироби.

алгоритм RSA

Шифрування з використанням публічного ключа

Шифрування за допомогою публічного ключа використовується повсюдно. Якщо ви хоча б раз оплачували щось в інтернеті, то вже користувалися цим методом (я сподіваюся!). Відразу ж виникає питання про те, як працює цей захист. Якщо я вводжу номер своєї кредитної картки, щоб щось купити, чому крім адресата ніхто не може підглянути ці відомості? Наведу метафору. Щоб відкрити сейф, вам потрібно ключ (або молоток, але, на щастя, сейфи і замки захищені від такого роду діячів). У шифруванні з використанням публічного ключа відбувається приблизно те ж саме. Ви показуєте замок на загальний огляд, але ключ від цього замка є тільки у обраних, а іншими методами відкрити двері практично неможливо.

RSA - один з алгоритмів, що реалізують вищезазначену схему. Крім того, ми можемо використовувати цей алгоритм для підтвердження автентичності нашої особистості. Якщо ви, використовуючи секретний ключ, відсилаєте комусь зашифроване повідомлення, адресат за допомогою публічного ключа може розшифрувати ваше послання. Ця технологія дозволяє підписувати повідомлення, і тим самим підтверджується справжність відправника.

Демо-програма на базі алгоритму RSA

Я написав невелику програму з реалізацією шифрування за алгоритмом RSA. За допомогою прапорів -t і -m (із зазначенням будь-якого цілого числа на ваш вибір) демонструються базові можливості шифрування повідомлення з використанням публічного ключа.

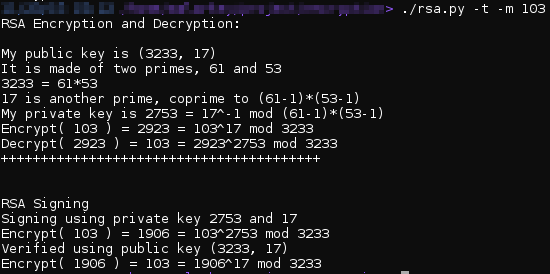
Малюнок 1: Процедура шифрування, дешифрування і цифрового підпису за допомогою алгоритму RSA

В наведеному вище прикладі показана покрокова схема використання суспільного телебачення і секретного ключа. Публічний ключ складається з двох чисел: (3233, 17). Перше число (3233) є результатом множення двох простих чисел (61 і 53). Друге число (17) - просте. Єдиний загальний множник двох чисел нашого ключа - одиниця. Далі ми генеруємо секретний ключ, використовуючи обрані раніше два простих числа. Потім ми можемо шифрувати і дешифрувати повідомлення за допомогою публічного і секретного ключа відповідно. Якщо ми хочемо підписати повідомлення, то використовуємо ключі в зворотному порядку (спочатку секретний, потім - публічний).

У програми є додаткові опції (див. Малюнок нижче), що дозволяють задавати власні ключі.

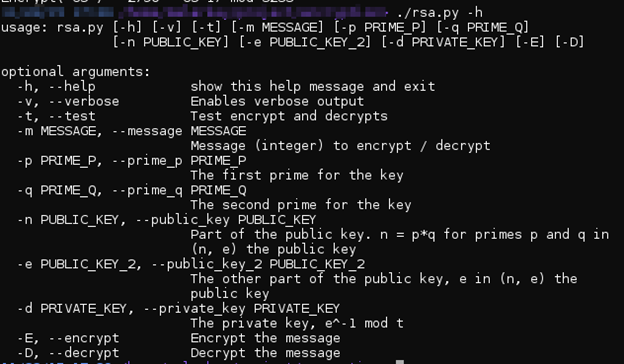
Малюнок 2: Інші опції демонстраційної програми

Один нюанс - програма працює некоректно, якщо повідомлення більше, ніж публічний ключ.

Математична сторона питання

RSA багато в чому схожий з алгоритмом Діффі-Хеллмана, оскільки і там і там використовується модулярная арифметика. Нижче по кроках розповідається, як генерується публічний і секретний ключ.

1. Вибираємо два простих числа p і q.
2. Обчислюємо n = p * q (частина публічного ключа).
3. Обчислюємо тотіент від n, t, який закінчується числом (p-1) * (q-1).
4. Вибираємо просте число e <t і перевіряємо, щоб t% e не було дорівнює 0 (e - друга частина публічного ключа).
5. Обчислюємо секретний ключ d = e ^ -1 mod t, де d * e mod t = 1.

Тепер по кроках розглянемо процес шифрування і дешифрування:

1. Щоб зашифрувати повідомлення, використовуємо формулу E = m ^ e mod n (m - повідомлення).
2. Щоб розшифрувати повідомлення, використовуємо формулу E ^ d mod n.

Доказ того, що Дешифровка (Шифровка (M)) = M наводиться в Вікіпедії . Тут ми ще більше занурюємося в математику і доведення теорем. Якщо ви не особливо підковані в цій області, просто спробуйте позапускать скрипт з різними ключами і повідомленнями і переконайтеся, що все працює коректно.

Ризикну припустити, що багатьом з вас цікаво, як зламати систему, побудовану на основі алгоритму RSA. Зловмисник знає числа n і e. Якщо зломщик зможе знайти число t, то вирахує секретний ключ. Завдання полягає в тому, щоб факторізовать публічний ключ. Однак целочисленная факторизация - досить складне завдання, і саме тому алгоритм RSA досить стійкий. Можливо, коли з'являться квантові машини, обчислити секретний ключ не становитиме особливих труднощів, але зараз достатньої довгий ключ зможе захистити наші дані.

додаткові роздуми

При читанні статті у вас, можливо, виникло наступне питання: «Як мені переконатись в тому, що отриманий публічний ключ саме ту людину, якій я хочу відіслати повідомлення?». Якщо ми можемо оприлюднити публічний ключ, то з таким же успіхом могли б поділитися і секретним ключем. Більш того, я не можу сходити в офіс Амазону і отримати від них публічний ключ. Я веду до того, що мені потрібно отримати цей ключ якимось чином. Інфраструктура відкритих ключів (Public Key Infrastructure, PKI) - технологія, що дозволяє управляти всіма цими ключами. Ми використовуємо шифрування для підтвердження наших ключів, призначених для шифрування (виходить замкнуте коло). Розглянути цю проблему в рамках однієї статті не вийде. Якщо ви хочете дізнатися подробиці, гугл вам на допомогу.

Крім того, алгоритм RSA досить повільний, і якщо комусь вдасться обчислити два простих числа, то весь трафік, що виходить від вас, буде розшифрований. Як захист можна запропонувати наступне. Пам'ятайте, як я говорив, що той же самий алгоритм можна використовувати для підпису повідомлень? Для обміну ключами ми можемо використовувати алгоритм Діффі-Хеллмана (див. Першу частину), а підписувати повідомлення за допомогою RSA. У підсумку наш ключ під час кожної нової сесії буде іншим. Використовуючи RSA, ми встановлюємо справжність адресата. В кінцевому рахунку, ми отримуємо алгоритм для обміну ключами і верифікації адресата. Коли-небудь я напишу програму, що реалізовує цю технологію.

Сподіваюся, ви подчерпнул для себе щось нове. Шифруйте і підписуйте свої повідомлення!

посилання

https://en.wikipedia.org/wiki/RSA_(cryptosystem)