Новости
- Вступ Працюючи на фінансових ринках, ми постійно зайняті пошуком системи, яка приносила б нам прибуток....
- Трохи про диверсифікацію
- параметричні методи
- Короткий огляд книги Вінса
Вступ
Працюючи на фінансових ринках, ми постійно зайняті пошуком системи, яка приносила б нам прибуток. При цьому, звичайно, хотілося б, щоб ця система була максимально стабільною і мала мінімальним ризиком. Щоб цього досягти, розробляються торгові системи, основний упор в яких зроблений на пошуку оптимальних точок входу / виходу. Створюються технічні індикатори та торгові сигнали, що вказують, коли купувати / продавати. Розроблена ціла система цінових моделей (фігур) для технічного аналізу. Разом з тим, як показує у своїй роботі "Математика управління капіталом" Ральф Вінс, розмір капіталу, який використовується для проведення угод, не менш важливий. Для оптимізації прибутку і, що не менш важливо, збереження депозиту потрібно визначитися з розміром лота, яким ми торгуємо.
Попутно в роботі Вінса спростовуються розхожі "псевдоконцепції". Наприклад, до таких концепцій можна віднести відоме правило "чим більше ризик, тим вище прибуток":
Потенційний прибуток - лінійна функція потенційного ризику. Це не вірно!
Наступна "помилкова концепція" - диверсифікація зменшує збитки. Але і це не так. За Винсу:
Вона може це зробити, але тільки до певної міри - набагато меншою, ніж вважає більшість трейдерів.
Основні положення
Для наочності розглянемо основні ідеї на прикладах. Припустимо, у нас є деяка умовна система з двох угод. Перша угода виграє 50%, а друга програє 40%. Якщо ми не реінвестуємо прибуток, то виграємо 10%, а якщо реінвестуємо - та ж послідовність операцій дає програш 10%. (P & L = Profit or Loss).
Номер угоди P & L без реінвестування Повний капітал
P & L з реинвестированием Повний капітал
100
100 1 +50 150
+50 150 2 -40 110
-60 90
При реінвестування прибутку виграшна система перетворилася в програшну. Неважко переконатися, що порядок угод не має значення. З цього прикладу видно, що при реінвестування капіталу ми не можемо діяти точно так же, як і при торгівлі з фіксованим лотом. Власне, пошук оптимального розміру лота при реінвестування і становить основу методу Вінса з управління капіталом.
Підемо від простого до складного - почнемо з підкидання монетки. Нехай в разі виграшу ми отримуємо 2 долари, а в разі програшу втрачаємо 1 долар. Імовірність програшу або виграшу дорівнює 1/2. Припустимо, у нас є 100 доларів. Тоді якщо ми поставимо на кін усе 100 доларів, наша потенційна прибуток буде 200 доларів. Але в разі програшу ми втратимо відразу всю суму і не зможемо далі продовжувати гру. При нескінченній грі - а саме така гра передбачається для оптимізації - ми гарантовано опинимося в програші.
Якби ми ставили не всю суму відразу, а якусь її частину - наприклад, 20 доларів з 100 - то в разі програшу у нас залишалися б гроші для продовження гри. Розглянемо послідовність можливих угод при різній частці капіталу на одну угоду. Початковий капітал всюди 100 доларів.
Угода P & L при К = 0.1 Капітал P & L при К = 0.2 Капітал P & L при К = 0.5 Капітал P & L при К = 0.7 Капітал P & L при К = 1 Капітал 100 100 100 100 100 +2 20 120 40 140 100 200 140 240 200 300 -1 -12 108 -28 112 -100 100 -168 72 -300 0 +2 21.6 129.6 44.8 156.8 100 200 100.8 172.8 0 0 -1 -12.96 116.64 -31.36 125.44 -100 100 -120.96 51.84 0 0 +2 23.33 139.97 50.18 175.62 100 200 72.58 124.42 0 0 -1 -14 125.97 -35.12 140.5 -100 100 -87.09 37.32 0 0 Разом 126 141 100 37 0
Як зазначалося вище, прибуток / збиток не залежить від послідовності операцій. Тому цілком коректно, що у нас прибуткові угоди чергуються зі збитковими.
Очевидно, що існує певний оптимальний коефіцієнт (дільник) при якому прибуток максимальна. Для простих випадків, коли ймовірність виграшу і ставлення прибуток / програш постійні, цей коефіцієнт знаходять за формулою Келлі:
f = ((B + 1) * P-1) / B
f - оптимальна фіксована частка, яку далі ми і будемо шукати;
P - ймовірність виграшу;
B - відношення виграш / програш.
Далі для зручності f буду називати просто коефіцієнтом.
Зрозуміло, що на практиці розмір і ймовірність виграшу постійно змінюються і формула Келлі непридатна. Тому для емпіричних даних коефіцієнт f знаходиться чисельними методами. Оптимізувати будемо прибутковість системи за довільним емпіричному потоку угод. Для прибутку за угодою Вінс застосовує термін HPR (holding period returns, або прибуток за період утримання позиції). Якщо угода принесла прибуток 10%, то HPR = 1 + 0.1 = 1.1. Отже, для однієї угоди HPR = 1 + f * Прибуток / (Максимальний можливий програш), де прибуток береться зі знаком плюс або мінус, залежно від того отриманий програш чи виграш. Фактично коефіцієнт f - це коефіцієнт максимальної можливої просадки. Щоб знайти оптимальний f, нам треба знайти максимум твори по всіх угодах max (HPR1 * HPR2 * ... * HPRn).
Напишемо програму знаходження f для довільного масиву даних.
Програма 1. Пошук оптимального f.
double PL [] = {9, 18, 7, 1, 10, - 5, - 3, - 17, - 7}; double Arr [] = {2, -1}; void OnStart () {SearchMaxFactor (Arr); // Або PL і будь-який інший масив} void SearchMaxFactor (double & arr []) {double MaxProfit = 0, K = 0; for (int i = 1; i <= 100; i ++) {double k, profit, min; min = MathAbs (arr [ArrayMinimum (arr)]); k = i * 0.01; profit = 1; for (int j = 0; j <ArraySize (arr); j ++) {profit = profit * (1 + k * arr [j] / min); } If (profit> MaxProfit) {MaxProfit = profit; K = k; }} Print ( "Optimal K", K, "Profit", NormalizeDouble (MaxProfit, 2)); }
Можна переконатися, що для випадку + 2, -1, + 2, -1 і т.д. f буде той же, що і отриманий за допомогою формули Келлі.
Майте на увазі, що оптимізація має сенс тільки для прибуткових систем - тобто систем, для яких математичне сподівання (середній прибуток) позитивне. Для збиткових систем оптимальне f = 0. Управління розміром лота не робить збиткову систему прибутковою. Навпаки, якщо в потоці немає збитків, тобто якщо все P & L> 0, оптимізація також не має сенсу, f = 1, і потрібно торгувати максимальним лотом.
Ми можемо, користуючись графічними можливостями MQL5, знайти не тільки максимальне значення f, а й подивитися всю криву розподілу прибутку в залежності від f. Нижче представлена програма, яка малює графік прибутку в залежності від коефіцієнта f.
Програма 2. Графік прибутку в залежності від f.
#property copyright "Orangetree" #property link "https://www.mql5.com" #property version "1.00" #include <Graphics \ Graphic.mqh> double PL [] = {2, - 1}; void OnStart () {double X [100] = {0}; for (int i = 1; i <= 100; i ++) X [i- 1] = i * 0.01; double Y [100]; double min = PL [ArrayMinimum (PL)]; if (min> = 0) {Comment ( "f = 1"); return;} min = MathAbs (min); int n = ArraySize (X); double maxX [1] = {0}; double maxY [1] = {0}; for (int j = 0; j <n; j ++) {double k = X [j]; double profit = 1; for (int i = 0; i <ArraySize (PL); i ++) {profit = profit * (1 + k * PL [i] / min); } Y [j] = profit; if (maxY [0] <profit) {maxY [0] = profit; maxX [0] = k; }} CGraphic Graphic; Graphic.Create (0, "Graphic", 0, 30, 30, 630, 330); CCurve * Curve = Graphic.CurveAdd (X, Y, ColorToARGB (clrBlue, 255), CURVE_LINES, "Profit"); Curve.LinesStyle (STYLE_DOT); CCurve * MAX = Graphic.CurveAdd (maxX, maxY, ColorToARGB (clrBlue, 255), CURVE_POINTS, "Maximum"); MAX.PointsSize (8); MAX.PointsFill (true); MAX.PointsColor (ColorToARGB (clrRed, 255)); Graphic.XAxis (). MaxLabels (100); Graphic.TextAdd (30, 30, "Text", 255); Graphic.CurvePlotAll (); Graphic.Update (); Print ( "Max factor f =", maxX [0]); }
Графік для {+ 2, -1} має вигляд:
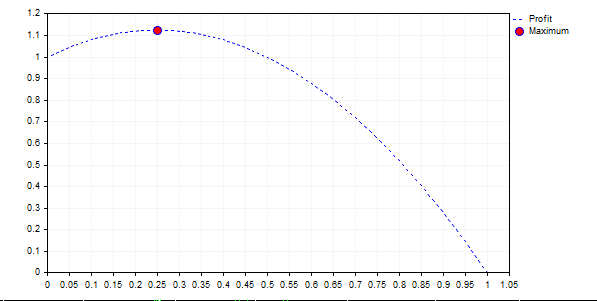
З отриманого графіка видно, що правило "чим більше ризик, тим більший прибуток" невірно. У всіх випадках, коли крива лежить нижче 1 (f> 0.5), ми в кінцевому підсумку отримаємо збиток, а при нескінченній грі - 0 на рахунку.
Тут є одна цікава протиріччя. Чим вище математичне очікування прибутку і стабільніше система, тим більше коефіцієнт f. Наприклад, для потоку {-1,1,1,1,1,1,1,1,1,1} коефіцієнт дорівнює 0.8, і про таку систему, здавалося б, можна тільки мріяти. Але коефіцієнт 0.8 означає, що максимальний допустимий збиток дорівнює 80%, і в один прекрасний день ви втратите 80% рахунку! Так, з точки зору математичної статистики це оптимальний розмір лота для максимального збільшення балансу, але чи готові ви до таких втрат?
Трохи про диверсифікацію
Припустимо, у нас є дві торгові стратегії А і Б з однаковим розподілом прибутків / збитків, наприклад ті ж (+ 2, -1). Для цих систем оптимальне f одно 0.25. Розглянемо випадки, коли системи мають кореляцію 1,0 і -1. Баланс рахунку будемо просто ділити порівну між цими системами.
Кореляція 1, f = 0.25
Система А Угода P & L Система Б Угода P & L Комбінований рахунок 50 50 100 2 25 2 25 150 -1 -18.75 -1 -18.75 112.5 2 28.13 2 28.13 168.75 -1 -21.09 -1 -21.09 126.56 прибуток 26.56
Як і можна було очікувати, цей варіант нічим не відрізняється від випадку торгівлі всім капіталом по одній стратегії. Тепер візьмемо випадок, коли кореляція дорівнює 0.
Кореляція 0, f = 0.25
Система А Угода P & L Система Б Угода P & L Комбінований рахунок 50 50 100 2 25 2 25 150 2 37.5 -1 -18.75 168.75 -1 -21.1 2 42.19 189.85 -1 -23.73 -1 -23.73 142.39
прибуток 42.39
Прибуток значно більше. І, нарешті, випадок кореляції -1.
Кореляція -1, f = 0.25
Система А Угода P & L Система Б Угода P & L Комбінований рахунок 50 50 100 2 25 -1 -12.5 112.5 -1 -14.08 2 28.12 126.56 2 31.64 -1 -15 142.38 -1 17.8 2 35.59 160.18
прибуток 60.18
У цьому випадку прибуток максимальна. На цих та подібних прикладах можна побачити, що в разі реінвестування прибутку диверсифікація дає кращі результати. Але також легко помітити, що вона не позбавляє від найгіршого випадку (в нашому прикладі найбільший збиток f = 0.25 від розміру балансу), за винятком випадку, коли системи мають кореляцію -1. На практиці таких систем з кореляцією рівно -1 не буває. Це аналогічно нагоди відкриття позицій по одному інструменту в різні боки. На підставі таких міркувань Вінс приходить до наступного висновку. Наведу її первісному вигляді цитату з книги.
Мораль така: диверсифікація, якщо вона зроблена правильно, є методом, який підвищує прибутку. Вона не обов'язково зменшує програші гіршого випадку, що абсолютно суперечить популярному поданням.
Кореляція і інша статистика
Перш ніж перейти до параметричних методів знаходження коефіцієнта f, розглянемо ще кілька характеристик потоку прибутків. Може трапитися так, що ми отримуємо серіювзаємозалежних результатів. За прибутковими операціями слідують прибуткові, а за збитковими - збиткові. Для виявлення подібних залежностей розглянемо два методи: знаходження автокорреляции ряду і серійний тест.
Серійний тест полягає в обчисленні показника, який називається рахунок Z. За змістом рахунок Z - це число стандартних відхилень, на яке дані відстоять від середнього значення нормального розподілу. Негативне значення Z говорить про те, що смуг (безперервних рядів прибутку / збитків) менше, ніж в нормальному розподілі, а значить, за прибутком найімовірніше слід збиток і навпаки. Формула для рахунку Z:
Z = (N (R-0.5) Х) / ((Х (Х-N)) / (N-1)) ^ (1/2)
або 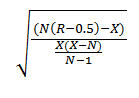
де:
- N - загальне число угод;
- R - загальна кількість серій;
- X = 2 * W * L, де
- W = загальне число виграшних угод в послідовності;
- L = загальне число програшних угод в послідовності.
Програма 3. Рахунок Z.
double Z (double & arr []) {int n = ArraySize (arr); int W, L, X, R = 1; if (arr [0]> 0) {W = 1; L = 0; } Else {W = 0; L = 1; } For (int i = 1; i <n; i ++) {if (arr [i]> 0) {W ++; if (arr [i- 1] <= 0) {R ++;}} else {L ++; if (arr [i- 1]> 0) {R ++;}}} X = 2 * W * L; double x = (n * (R- 0.5) -X); double y = X * (Xn); y = y / (n- 1); double Z = (n * (R- 0.5) -X) / pow (y, 0.5); Print (Z); return Z; }
Рахунок Z розраховується Тестером Стратегій, де в звіті (Бектест) він так і називається "Z-рахунок».
Автокорреляция - статична взаємозв'язок між послідовностями величин одного ряду, взятими із зсувом. Для ряду {1,2,3,4,5,6,7,8,9,10}, це кореляція між рядами {1,2,3,4,5,6,7,8,9} і {2 , 3,4,5,6,7,8,9,10}. Нижче розглянута програма для знаходження автокорреляции.
Програма 4. Автокорреляция.
double AutoCorr (double & arr []) {int n = ArraySize (arr); double avr0 = 0; for (int i = 0; i <n- 1; i ++) {avr0 = avr0 + arr [i]; } Avr0 = avr0 / (n- 1); double avr1 = 0; for (int i = 1; i <n; i ++) {avr1 = avr1 + arr [i]; } Avr1 = avr1 / (n- 1); double D0 = 0; double sum = 0,0; for (int i = 0; i <n- 1; i ++) {sum = sum + (arr [i] -avr0) * (arr [i] -avr0); } D0 = MathSqrt (sum); double D1 = 0; sum = 0,0; for (int i = 1; i <n; i ++) {sum = sum + (arr [i] -avr1) * (arr [i] -avr1); } D1 = MathSqrt (sum); sum = 0,0; for (int i = 0; i <n- 1; i ++) {sum = sum + (arr [i] -avr0) * (arr [i + 1] -avr1); } If (D0 == 0 || D1 == 0) return 1; double k = sum / (D0 * D1); return k; }
Якщо результати угод взаємопов'язані, то торгову стратегію має сенс скорегувати. Кращі результати вийдуть, якщо ми будемо використовувати два різних коефіцієнта - f1 і f2 - для прибутків і збитків. Для цього випадку буде написаний окремий модуль управління капіталом на MQL5.
параметричні методи
Оптимізуючи параметри системи, ми можемо використовувати два підходу. Перший - емпіричний, заснований безпосередньо на експериментальних даних, коли ми оптимізуємо параметри під конкретні результати. І другий - параметричний, заснований на функціональних або статичних залежностях. Приклад параметричного методу - знаходження оптимального коефіцієнта з формули Келлі.
Для знаходження оптимального коефіцієнта Вінс пропонує використовувати розподілу отриманих прибутків. Спочатку він розглядає нормальний розподіл, як найбільш вивчене і поширене, потім конструює узагальнене розподіл.
Завдання формулюється так. Припустимо, наші прибутки / збитки розподілені відповідно до нормального (або - в загальному випадку - з будь-яким іншим) розподілом. Знайдемо оптимальний коефіцієнт f для цього розподілу. У разі нормального розподілу нам з експериментальних даних досить знайти середнє значення потоку PL (profit / loss) і стандартне відхилення. Ці два параметри повністю характеризують нормальний розподіл.
Нагадаю формулу щільності нормального розподілу:
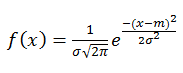
де
- σ - стандартне відхилення
- m - математичне очікування (середнє значення).
Сама ідея мені сподобалася. За допомогою емпіричних даних знайти характер розподілу прибутків / збитків. І вже з цієї функції, до якої прагнуть результати, знаходити параметр f, тим самим уникаючи впливу випадкових значень. На жаль, на практиці все не так просто. Але все по порядку. Спочатку про сам метод.
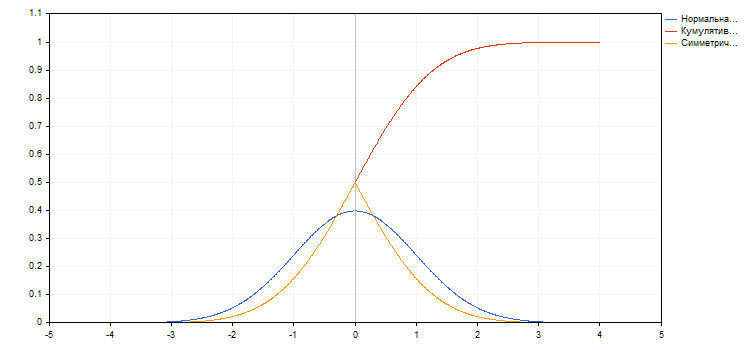
На графіку синім кольором побудований графік щільності нормального розподілу, де середнє значення дорівнює нулю, а стандартне відхилення - одиниці. Червоним кольором відображається інтеграл цієї функції. Це кумулятивна вірогідність, то є ймовірність того, що значення менше або дорівнює заданому Х. Її прийнято позначати F (x). Помаранчевий графік - ймовірність того, що значення менше або дорівнює х при х <0 і що значення більше або дорівнює х при х> 0 (F (x) '= 1-F (x), при х> 0. Всі ці функції добре відомі і їх значення легко отримати.
Нам потрібно знайти найбільше середнє геометричне угод, розподілених за цим законом. Для цього Вінс пропонує наступні дії.
Спочатку знаходимо характеристики розподілу - середнє значення і стандартне відхилення. Потім вибираємо "довірчий інтервал" або ширину відсікання, який виражається в стандартних відхиленнях. Зазвичай вибирають інтервал 3σ. Значення більше 3σ відсікаються. Потім даний інтервал розбивається на відрізки і знаходяться "асоційовані значення" прибутків / збитків (PL). Наприклад, для σ = 1 і m = 0 значення асоційованих PL на краях інтервалу будуть m + - 3σ = +3 і -3. Якщо ми розбили інтервал на відрізки довжиною 0.1σ, то асоційовані PL будуть -3, -2.9, -2.8 ... 0 ... 2.8, 2,9, 3. І саме для цього потоку PL ми знаходимо оптимальне f.
Так як різні значення PL мають різну ймовірність, то для кожного значення знаходиться його "асоційована ймовірність" P. Після цих перетворень шукається максимум творів:
HPR = (1+ PL * f / maxLoss) ^ P, де maxLoss - максимальний збиток (по модулю).
Тут Вінс пропонує в якості асоційованого ймовірності брати кумулятивну ймовірність, яка у нас на графіку показана помаранчевим кольором F '(x).
Було б логічно, якби кумулятивна ймовірність бралася тільки для крайніх значень, а для інших значень P = F '(x) -F' (y), де х і у - значення F (x) на краях інтервалу.
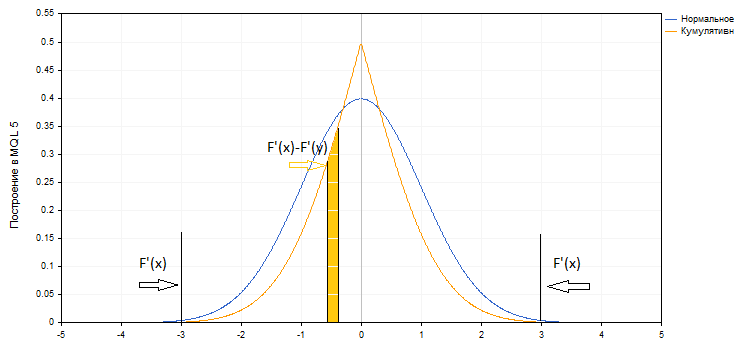
Тоді множник HPR = (1+ PL * f / maxLoss) ^ P був би своєрідним "зваженим значенням". Сумарна ймовірність цих значень, як і належить, була б дорівнює одиниці. У книзі Вінс визнає, що отримані таким чином результати не збігаються з результатами, отриманими на фактичних даних. Він відносить це до обмеженості вибірки і відмінності фактичного розподілу від нормального. Стверджується, що при збільшенні числа елементів і розподілі їх по нормальному закону параметричні і фактичні значення оптимального коефіцієнта f будуть сходитися.
Цікаво, що в розібраному по його методу прикладі сумарна ймовірність виявляється рівною 7.9. Ччтоби знайти середнє геометричне, він просто витягує з результату корінь 7.9-го ступеня. По всій видимості, для такого підходу є суворе математичне обґрунтування.
Ми ж, маючи в своєму розпорядженні такий інструмент, як MQL5, можемо все це легко перевірити. Для цього у нас є бібліотека Normal.mqh, яка знаходиться за адресою <Math \ Stat \ Normal.mqh>.
Для експериментів я зробив два варіанти: в точності як у Вінса і описаний вище. Для знаходження "асоційованих ймовірностей" використовується бібліотечна функція MathCumulativeDistributionNormal (PL, mean, stand, ProbCum).
Програма 5. Пошук оптимального f по нормальному розподілу (по Винсу).
#property copyright "Copyright 2017, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <Math \ Stat \ Math.mqh> #include <Math \ Stat \ Normal.mqh> input double N = 3; input int M = 60; void OnStart () {double arr [10000]; bool ch = MathRandomNormal (1, 8, 10000, arr); double mean = MathMean (arr); double stand = MathStandardDeviation (arr); double PL []; ArrayResize (PL, M + 1); for (int i = 0; i <M + 1; i ++) {double nn = -N + 2.0 * i * N / M; PL [i] = stand * nn + mean; } Double ProbCum []; ArrayResize (ProbCum, M + 1); ch = MathCumulativeDistributionNormal (PL, mean, stand, ProbCum); for (int i = 0, j = 0; i <M + 1; i ++) {if (i <= M / 2) continue; else j = Mi; ProbCum [i] = ProbCum [j]; } Double SumProb = 0; for (int i = 0; i <M + 1; i ++) {SumProb = SumProb + ProbCum [i]; } Print ( "SumProb", SumProb); double MinPL = PL [ArrayMinimum (PL)]; double min = arr [ArrayMinimum (arr)]; double f = 0.01, HPR = 1, profit = 1; double MaxProfit = 1, MaxF = 0; for (int k = 0; k <1000; k ++) {f = k * 0.001; profit = 1; for (int i = 0; i <M + 1; i ++) {HPR = pow ((1-PL [i] / MinPL * f), ProbCum [i]); profit = HPR * profit; } If (MaxProfit <profit) {MaxF = f; MaxProfit = profit; }} Print ( "Profit Vince"); Print (MaxF, "", pow (MaxProfit, 1 / SumProb), "", Profit (MaxF, min, arr)); MaxF = 0; MaxProfit = 1; for (int k = 0; k <1000; k ++) {f = k * 0.001; profit = Profit (f, min, arr); if (MaxProfit <profit) {MaxF = f; MaxProfit = profit; }} Print ( "------ MaxProfit -------"); Print (MaxF, "", MaxProfit); } Double Profit (double f, double min, double & arr []) {if (min> = 0) {return 1.0; Alert ( "min> = 0"); } Double profit = 1; int n = ArraySize (arr); for (int i = 0; i <n; i ++) {profit = profit * (1-arr [i] * f / min); } Return profit; }
Код програми знаходиться у файлі Vince.mq5
У цій програмі знаходиться коефіцієнт з нормального розподілу і потім - для порівняння - за фактичними даними. Другий варіант відрізняється тільки масивом "асоційованих" ймовірностей і PL.
Програма 6.
............................................. double ProbDiff []; ArrayResize (ProbDiff, M + 2); double PLMean []; ArrayResize (PLMean, M + 2); ProbDiff [0] = ProbCum [0]; ProbDiff [M + 1] = ProbCum [M]; PLMean [0] = PL [0]; PLMean [M + 1] = PL [M]; for (int i = 1; i <M + 1; i ++) {ProbDiff [i] = MathAbs (ProbCum [i] -ProbCum [i- 1]); PLMean [i] = (PL [i] + PL [i- 1]) / 2; } ..............................................
Код програми знаходиться у файлі Vince_2.mq5
Тут PLMean [i] = (PL [i] + PL [i- 1]) / 2; - середнє значення PL на відрізку розбиття, ProbDiff [] - значення ймовірності того, що величина знаходиться в заданому інтервалі. По краях значення відсікаються (можливо стоп-лоссом або тейк-профітом), тому ймовірність на краях просто дорівнює кумулятивної ймовірності.
Обидві програми працюють приблизно однаково і видають приблизно однакові результати. Виявилося, що відповідь сильно залежить від N - ширини відсікання ( "довірчого інтервалу"). Причому, що найсумніше, при збільшенні N коефіцієнт f, отриманий з нормального розподілу, прагне до 1. Теоретично, чим ширше інтервал "відсікання", тим точніше повинен вийти результат. На практике це не так.
Так може виходити через що накопичується помилки. Експоненціальна функція досить швидко убуває, і нам доводиться мати справу з досить малими величинами - HPR = pow ((1 -PL [i] / MinPL * f), ProbCum [i]). Можливо, що і сама методика десь містить помилку. Але для практичного застосування це не принципово. У будь-якому випадку, для коректної роботи нам потрібно якимось чином "підганяти" параметр N, який сильно впливає на результат.
Зрозуміло, що реальний потік PL відрізняється від нормального розподілу. У зв'язку з цим Вінс створює узагальнене розподіл з параметрами, що імітують характеристики будь-якого довільного розподілу. Додаються параметри, що задають різні моменти розподілу (середнє значення, ексцес, ширину, асиметрію). Потім передбачається за допомогою чисельних методів знайти ці параметри для емпіричних даних і побудувати функцію розподілу потоку PL.
Так як результати експериментів з нормальним розподілом мені не сподобалися, чисельні розрахунки з узагальненим розподілом я вирішив не проводити. Наведу ще аргумент на користь своїх сумнівів.
Вінс стверджує, що параметричні методи набагато могутніше. Адже зі збільшенням числа експериментів дані будуть прагнути до теоретичних результатів, так як коефіцієнт, отриманий за вибіркою, неточний внаслідок обмеженості вибірки. Але параметри у випадку з нормальним розподілом (середнє значення і стандартне відхилення) ми отримуємо саме з цієї обмеженою вибірки. Неточність розрахунку характеристик розподілу точно така ж. Потім ця неточність тільки збільшується через що накопичується помилки в збільшуються обчисленнях. При цьому, як з'ясовується, результати в практичній реалізації ще і залежать від ширини відсікання. Так як на практиці розподіл не є нормальним, ми додаємо ще одну ланку - пошук функції розподілу, знову ж заснований на тих же самих емпіричних кінцевих даних. Додаткова ланка тягне за собою додаткову похибка обчислень.
Дозволю висловити своє скромне думку. Параметричний підхід являє собою ілюстрацію того, що красиві в теорії ідеї не завжди так само красиві і на практиці.
Короткий огляд книги Вінса
Настав час коротко резюмувати роботу Вінса "Математика управління капіталом". Книга являє собою суміш огляду методів статистики з різними методами пошуку оптимального коефіцієнта f. У ній розглядається досить великий набір тем: модель Марковіца управління портфелем, тест Колмогорова-Смирнова для розподілів, модель оцінки фондових опціонів Блека-Шоулса і навіть методи вирішення систем рівнянь. Все це виходить далеко за рамки окремої статті. Але головне - всі ці методи розглядаються в контексті пошуку оптимального коефіцієнта f. Тому я вирішив на них не зупинятися, а перейти до практичної реалізації даного методу. Реалізація буде у вигляді модулів для майстра MQL5.
Модуль майстра MQL5
В цілому реалізація модуля подібна до вже наявному стандартним модулем MoneyFixedRisk. Там розмір лота знаходиться через задається стоп-лосс. Для наочності залишимо стоп-лосс незалежним і задамо коефіцієнт f і максимальний збиток в явному вигляді через вхідні параметри.
Для початку створимо в директорії Include / Expert нову папку для своїх модулів - наприклад, MyMoney. У ній створимо файл MoneyF1.mql.
Всі торгові модулі складаються з набору стандартних частин: класу торгового модуля і його спеціального опису (дескриптора класу).
Клас, як правило, містить:
- конструктор;
- деструктор;
- функції установки вхідних параметрів;
- функцію перевірки введених значень параметрів ValidationSettings (void);
- м етод визначення обсягу позиції CheckOpenLong (double price, double sl) і CheckOpenShort (double price, double sl).
Назвемо наш клас CMoneyFactor
class CMoneyFactor: public CExpertMoney {protected: double m_factor; double m_max_loss; public: CMoneyFactor (void); ~ CMoneyFactor (void); void Factor (double f) {m_factor = f;} void MaxLoss (double point) {m_max_loss = point;} virtual bool ValidationSettings (void); virtual double CheckOpenLong (double price, double sl); virtual double CheckOpenShort (double price, double sl); }; void CMoneyFactor :: CMoneyFactor (void): m_factor (0.1), m_max_loss (100) {} void CMoneyFactor :: ~ CMoneyFactor (void) {}
Максимальний програш в пунктах заданий типом double для відповідності стандартним модулям. Пов'язано це з тим, що в інших модулях, що поставляються разом з дистрибутивом, стоп-лосс і тейк-профіт задаються в пунктах обумовленими в базовому класі ExpertBase.mqh
ExpertBase.mqh int digits_adjust = (m_symbol. Digits () == 3 || m_symbol. Digits () == 5)? 10: 1; m_adjusted_point = m_symbol. Point () * digits_adjust;
Тобто для котирувань з п'ятьма і трьома знаками після коми один пункт дорівнює 10 * Point (). 105 пунктів в сенсі Point () рівні 10.5 пунктам в стандартних модулях для MQL5.
Функції Factor (double f) і MaxLoss (double point) у станавливаются вхідні параметри і повинні називатися так само, як потім будуть описані в дескрипторі модуля.
Функція перевірки коректності введених параметрів:
bool CMoneyFactor :: ValidationSettings (void) {if (! CExpertMoney :: ValidationSettings ()) return (false); if (m_factor <0 || m_factor> 1) {Print (__FUNCTION__ + "Розмір коефіцієнта повинен бути в межах від 0 до 1"); return false; } Return true; }
Тут ми перевіряємо, щоб значення коефіцієнта було від 0 до 1.
І нарешті, самі функції визначення обсягу позиції. Для відкриття в "лонг":
double CMoneyFactor :: CheckOpenLong (double price, double sl) {if (m_symbol == NULL) return (0.0); double lot; double loss; if (price == 0.0) price = m_symbol. Ask (); loss = -m_account.OrderProfitCheck (m_symbol.Name (), ORDER_TYPE_BUY, 1.0, price, price - m_max_loss * m_adjusted_point); double stepvol = m_symbol.LotsStep (); lot = MathFloor (m_account.Balance () * m_factor / loss / stepvol) * stepvol; double minvol = m_symbol.LotsMin (); if (lot <minvol) lot = minvol; double maxvol = m_symbol.LotsMax (); if (lot> maxvol) lot = maxvol; return (lot); }
Тут максимальний збиток знаходиться за допомогою бібліотечного методу класу CAccountInf - OrderProfitCheck (). Потім додана перевірка лота на його відповідності дозволеним граничних значень - мінімального і максимального.
На початку кожного модуля йде його опис (дескриптор), необхідне компілятору для його розпізнавання.
Для експериментів цей модуль можна скомпілювати з будь-яким наявним модулем торгових сигналів. Попередньо можна обраний модуль торгових сигналів скомпілювати з модулем управління капіталом з фіксованим лотом. Отримані результати використовуємо для знаходження максимального збитку і потоку PL. Потім за цими результатами знайдемо оптимальний фактор f з допомогу Програми 1. Таким чином за експериментальними даними можна знайти оптимальний f. Інший спосіб - знайти оптимальний f безпосередньо з отриманого радника на основі нашого модуля шляхом його оптимізації. У мене результати розходяться лише на +/- 0.01. Це пов'язано з похибкою обчислень, наприклад, через заокруглень.
Код модуля знаходиться в файлі MoneyF1.mqh.
Може трапитися так, що потік наших прибутків / збитків має значиму автокореляцію. Це можна з'ясувати за допомогою наведених раніше програм розрахунку "рахунку Z" і автокореляції. Тоді має сенс задати два коефіцієнта - f1 і f2. Перший застосовується після прибуткових операцій, другий - після збиткових. Напишемо для даної стратегії другий модуль управління капіталом. Коефіцієнти потім можна знаходити за допомогою оптимізації, а можна - безпосередньо за даними потоку прибутків / збитків для тієї ж стратегії з фіксованим лотом.
Програма 7. Визначення оптимальних f1 і f2 по потоку прибутку / збитку.
void OptimumF1F2 (double & arr []) {double f1, f2; double profit = 1; double MaxProfit = 0; double MaxF1 = 0, MaxF2 = 0; double min = MathAbs (arr [ArrayMinimum (arr)]); for (int i = 1; i <= 100; i ++) {f1 = i * 0.01; for (int j = 1; j <= 100; i ++) {f2 = j * 0.01; profit = profit * (1 + f1 * arr [0] / min); for (int n = 1; n <ArraySize (arr); n ++) {if (arr [n- 1]> 0) {profit = profit * (1 + f1 * arr [n] / min);} else {profit = profit * (1 + f2 * arr [n] / min);}} if (MaxProfit <profit) {MaxProfit = profit; MaxF1 = i; MaxF2 = j; }}}
Відповідно, для майстра MQL5 потрібно переробити основні функції модуля управління капіталом. По-перше, додамо ще один параметр - f2 - і його перевірку. По-друге, переробимо функції CheckOpenLong () і CheckOpenShort (). Для визначення фінансового результату попередньої угоди додамо функцію CheckLoss ().
double CMoneyTwoFact :: CheckLoss () {double lot = 0,0; HistorySelect (0, TimeCurrent ()); int deals = HistoryDealsTotal (); CDealInfo deal; if (deals == 1) return 1; for (int i = deals- 1; i> = 0; i--) {if (! deal.SelectByIndex (i)) {printf (__FUNCTION__ + ": помилка вибору угоди за індексом"); break; } If (deal. Symbol ()! = M_symbol.Name ()) continue; lot = deal.Profit (); break; } Return (lot); }
Функції CheckOpenLong () CheckOpenShort ():
double CMoneyTwoFact :: CheckOpenLong (double price, double sl) {double lot = 0,0; double p = CheckLoss (); double loss; if (price == 0.0) price = m_symbol. Ask (); if (p> 0) {loss = -m_account.OrderProfitCheck (m_symbol.Name (), ORDER_TYPE_BUY, 1.0, price, price - m_max_loss * m_adjusted_point); double stepvol = m_symbol.LotsStep (); lot = MathFloor (m_account.Balance () * m_factor1 / loss / stepvol) * stepvol; } If (p <0) {loss = -m_account.OrderProfitCheck (m_symbol.Name (), ORDER_TYPE_BUY, 1.0, price, price - m_max_loss * m_adjusted_point); double stepvol = m_symbol.LotsStep (); lot = MathFloor (m_account.Balance () * m_factor2 / loss / stepvol) * stepvol; } Return (lot); } Double CMoneyTwoFact :: CheckOpenShort (double price, double sl) {double lot = 0,0; double p = CheckLoss (); double loss; if (price == 0.0) price = m_symbol. Ask (); if (p> 0) {loss = -m_account.OrderProfitCheck (m_symbol.Name (), ORDER_TYPE_SELL, 1.0, price, price + m_max_loss * m_adjusted_point); double stepvol = m_symbol.LotsStep (); lot = MathFloor (m_account.Balance () * m_factor1 / loss / stepvol) * stepvol; } If (p <0) {loss = -m_account.OrderProfitCheck (m_symbol.Name (), ORDER_TYPE_SELL, 1.0, price, price + m_max_loss * m_adjusted_point); double stepvol = m_symbol.LotsStep (); lot = MathFloor (m_account.Balance () * m_factor2 / loss / stepvol) * stepvol; } Return (lot); }
Повний код модуля знаходиться в файлі MoneyF1F2.mqh.
Як згадувалося вище, в цілому концепція управління капіталом по Винсу крутиться навколо оптимального коефіцієнта f. Тому для прикладу двома модулями цілком можна обмежитися. Хоча можна винайти і будь-які додаткові варіації. Наприклад, додати елементи Мартінгейла.
Прикріплені файли
У файлі Programs.mq5 знаходяться коди програм, використаних в статті. Додана сюди і програма для читання даних з файлу void ReadFile (string file, double & arr []). Вона потрібна для знаходження коефіцієнтів f по потоку прибутків / збитків з тестера стратегій. Можна, звичайно, підійти до справи ґрунтовно і написати цілий клас для парсинга звітів, як це зроблено в статті "Розкладаємо входи за індикаторами" . Але це ціла окрема програма зі своїми класами.
На мій погляд, простіше зробити так. Проганяємо стратегію з фіксованим лотом в тестері стратегій. Зберігаємо звіт тестера у вигляді Open XML (MS Office Excel). До колонці "прибуток" додаємо "своп" та "комісія" - отримуємо потік прибутку PL. Окремо цю колонку зберігаємо в текстовий файл або файл csv. Отримуємо набір рядків, що складаються з окремих результатів кожної угоди. Ці результати додана функція ReadFile () читає в масив arr []. Таким нескладним шляхом ми можемо знайти оптимальний f за даними будь-якої стратегії з фіксованим лотом.
У файлах Vince.mq5 і Vince_2.mq5 знаходяться вихідні параметричних методів знаходження оптимальних коефіцієнтів, розглянуті в статті.
Файли MoneyF1.mqh і MoneyF1F2.mqh вихідні торгових модулі управління капіталом.
Архівований файл містить всі ці файли, структуровані відповідно до їх розташуванням в MetaEditor.
Так, з точки зору математичної статистики це оптимальний розмір лота для максимального збільшення балансу, але чи готові ви до таких втрат?Digits () == 5)?