1. рекурсія Основні визначення
2. Прості приклади використання рекурсії
3. Графічні зображення рекурсивних викликів
4. Приклади використання рекурсії
5. Доказ завершимость рекурсії
6. Форми рекурсивних підпрограм
7. Приклади поганого і хорошого використання рекурсії
8. Рекурсивний спосіб обчислення чисел Фібоначчі, побудований за ітераційного алгоритму
9. Приклад хорошого використання рекурсії - ханойські вежі
10. Швидке сортування
11. код програми
12. Асимптотична оцінка складності
13. Генерація всіх перестановок
14. Генерація всіх підмножин
15. Перебір з поверненням (backtracking)
16. Питання про обході конем шахової дошки

рекурсія

Основні визначення

Рекурсією називається визначення об'єкта через такий же об'єкт.

Приклад.

(1) <Список> :: = <Число> | <Список> ',' <Число>

В даному прикладі рекурсивної частиною визначення є "<Список> ',' <Число>".

Зауваження 1. Рекурсивне визначення, будучи кінцевим, визначає безліч об'єктів.

Зауважимо також, що <Список> можна визначити і по-іншому:

(2) <Список> :: = <Число> | <Число> ',' <Список>

Визначення (1) називають леворекурсівним, а (2) - праворекурсівним.

Зауваження 2. У рекурсивном визначенні обов'язково (!!!) має бути присутня нерекурсівние частина.

Рекурсивне визначення може бути непрямим:

по одній з гілок рекурсивного визначення згадується об'єкт, у визначенні якого, в свою чергу, за однією з гілок визначається вихідний об'єкт.

Приклад.

<Оператор> :: = <присвоювання> | <Складовою оператор> <присвоювання> :: = <змінна>: = <вираз> <складовою оператор> :: = begin <список операторів> end <список операторів> :: = <порожньо> | <Оператор>; <Список операторів>

В даному прикладі є як пряме, так і непряме рекурсивне визначення.

У програмуванні під рекурсією розуміється:

• виклик з підпрограми самої себе (пряма рекурсія)
• виклик з підпрограми іншої підпрограми, яка викликає вихідну (непряма рекурсія)

При непрямої рекурсії обов'язково використання випереджаючого оголошення за допомогою ключового слова forward:

procedure q; forward; // випереджальне визначення procedure p; begin ... q; ... end; procedure q; begin ... p; ... end;

Прості приклади використання рекурсії

Приклад 1.

procedure p (i: integer); begin write (i, ''); p (i + 1); end;

При виклику цієї процедури станеться рекурсивне зациклення, тому що рекурсивний виклик виробляється безумовно.

Висновок. Щоб рекурсивного зациклення не відбулося, рекурсивний виклик повинен відбуватися не безумовно, а по якомусь умові, яке щоразу змінюється і при якомусь рекурсивном виклик стає хибним (так зване умова продовження рекурсії).

Виправимо нашу процедуру у відповідності зі зробленим висновком:

procedure p (i: integer); begin write (i, ''); if i <5 then p (i + 1); end;

При виклику p (0) буде виведено:

0 1 2 3 4 5

Графічно, рекурсивні виклики можна зобразити так:

Процес послідовних рекурсивних викликів підпрограми з самої себе називається рекурсивним спуском.
Процес повернення з рекурсивних викликів називається рекурсивним поверненням.

В даному прикладі числа виводяться на рекурсивном спуску (тобто в прямому порядку).
Однак, щоб дії виконувалися в зворотному порядку, їх потрібно викликати на рекурсивном повернення.

Приклад 2. вивести

0 1 2 3 4 5 4 3 2 1 0

Рішення:

procedure p (i: integer); begin write (i, ''); if i <5 then then begin p (i + 1); write (i, ''); end; end;

Максимальна глибина рекурсивних викликів називається глибиною рекурсії.
Поточна глибина називається поточним рівнем рекурсії.

Зауваження. Чим більше глибина рекурсії, тим більше накладні витрати по пам'яті.

Графічні зображення рекурсивних викликів

Одне графічне зображення у нас вже було. Згадаймо його:

procedure p (i: integer); begin write (i, ''); if i <5 then p (i + 1); end;

Розглянемо більш детально виклик p (0) процедури

procedure p (i: integer); begin write (i, ''); if i <2 then p (i + 1); end;

Згадаймо, що:

• Програмний стек - це безперервна область пам'яті, що виділяється програмі, зокрема, для розміщення в ній викликаються підпрограм.
• При кожному виклику підпрограми на стек кладеться її запис активації (ЗА), а при поверненні - знімається зі стека.

Т.ч. на стеку фактично зберігаються всі значення змінної i.

Зауваження 1. Оскільки при кожному рекурсивном виклик на стек поміщається ЗА, то при великій глибині рекурсії програмний стек може переповниться, і програма завершиться з помилкою.
Це станеться тим швидше, чим більше сумарний обсяг формальних параметрів і локальних змінних.

Тому наступний код - дуже поганий !!!

procedure p (i: integer); var a: array [1..1000] of real; begin ... p (i + 1); ... end;

Зауваження 2. Накладні витрати на приміщення на стек ЗА, зняття ЗА зі стека, а також привласнення значень формальним параметрам на стеку досить великі.
Тому якщо є просте нерекурсівние рішення (ітераційне), то слід використовувати саме його.

Зауваження 3. Будь-яку рекурсию можна замінити итерацией.

Приклади використання рекурсії

Приклад 1. Знайти n! = N (n - 1) (n - 2) ... 2 * 1
Очевидно, визначити n! можемо наступним чином:

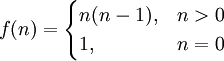
Тоді рішення має вигляд:

function nfact (n: integer): integer; begin if n = 0 then Result: = 1 else Result: = n * nfact (n - 1); end;

Однак, зауважимо, що повертається значення не визначене для n <0.
Як мінімум, можна замінити умова n = 0 на n <= 0, але, в такому випадку, ми отримаємо невірний результат, тому що факторіал взагалі не визначений для негативних чисел.
Очевидно, необхідно за допомогою затвердження перевірити коректність вхідного параметра (Assert (n> = 0)). Але його використання при кожному рекурсивном виклик накладно. Тому можна "обернути" рекурсивную підпрограму, наприклад, так:

function nfact (n: integer): integer; function nfactRecur (n: integer): integer; begin if n = 0 then Result: = 1 else Result: = n * nfact (n - 1); end; begin Assert (n> = 0); Result: = nfactRecur (n); end;

Глибина рекурсії цього алгоритму дорівнює n.

Приклад 2. Знайти 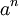. Дамо рекурсивне визначення:

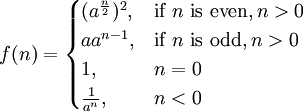
function power (a: real; n: integer): real; begin if n = 0 then Result: = 1 else if n <0 then Result: = 1 / power (a, - n) else // n> 0 if n mod 2 = 0 then Result: = sqr (power (a, n div 2)) else Result: = a * power (a, n - 1); end;

Глибина рекурсії дорівнює:

Приклад 3. Знаходження мінімального елемента в масиві. Визначити цей елемент можемо як мінімальний (один елемент, мінімальний з масиву без цього елемента), тобто рекурсивне визначення наступне:

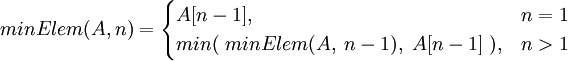
Відповідно до цього маємо рішення:

function MinElem (A: array of integer; n: integer): integer; begin if n = 1 then Result: = A [0] else Result: = min (MinElem (A, n - 1), A [n - 1])); end;

Глибина рекурсії дорівнює n - 1.

Ясно, що це не дуже хороший результат.
Можна значно зменшити глибину, якщо шукати мінімальний серед приблизно рівних частин масиву. Тобто потрібно поділити масив навпіл, знайти в кожній половині мінімальні елементи і порівняти їх. Пошук в половині здійснюється подібним же чином, і розподіл проводиться до тих пір, поки в підмасиві не залишиться один елемент.
Можна ще трохи оптимізувати цей алгоритм - якщо в підмасиві два елементи, досить повернути мінімальний з них.
Тепер знання кількості елементів недостатньо: необхідно знати, серед яких елементів масиву вести пошук. Тому будемо в якості параметрів передавати ліву (l) і праву (r) кордону подмассивов.
Дамо нове рекурсивне визначення:

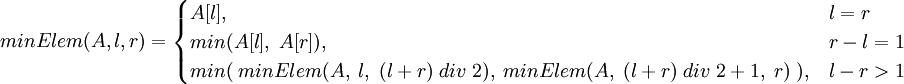
Рішення:

function MinElem (a: array of integer; l, r: integer): integer; begin if l = r then // якщо всього один елемент Result: = a [l] else if r - l = 1 then // якщо шукаємо мінімум з двох елементів Result: = min (a [l], a [r]) else begin var mid: = (l + r) div 2; Result: = min (MinElem (a, l, mid), MinElem (a, mid + 1, r)); end; end;

Глибина рекурсії такого алгоритму вже приблизно дорівнює 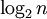(За кількістю ступенів).

Приклад 4. Висновок однозв'язного лінійного списку на екран.
Згадаймо, як виглядає список:

Рішення:

procedure Print <T> (h: Node <T>); begin if h = nil then exit; write (h. data, ''); Print (h. Next); end;

Глибина рекурсії дорівнює довжина списку - 1

Рекурсія називається кінцевий, якщо рекурсивний виклик є останнім в підпрограмі.

Кінцева рекурсія найбільш легко перетворюється в ітеративний алгоритм:

while h <> nil do begin write (h. data, ''); h: = h. next; end;

Доказ завершимость рекурсії

Додамо до рекурсивної процедури цілий параметр n:

p (n, ...);

Якщо при кожному рекурсивном виклик параметр n зменшується отримаємо виклики

p (n) p (n - 1) p (n - 2) p (n - 3)

І якщо рекурсія завершується при n <= 0, то це є доказом завершимость рекурсії.

Дійсно, на кожному наступному рівні рекурсії n стає менше.
Оскільки при n <= 0 рекурсивних викликів немає, то число рекурсивних викликів звичайно.

Стверджувати, що рекурсія завершимость, можна не завжди.
Приклад.

procedure p (n); begin if n <= 0 then exit else p (Random (2 * n) - n + 1); end;

Форми рекурсивних підпрограм

1. Дія виконується на рекурсивном спуску

p (n) S (n) if B (n) then p (n - 1)

2. Дія виконується на рекурсивном повернення

p (n) if B (n) then p (n - 1) S (n)

3. Дія виконується і на рекурсивном спуску і на рекурсивном повернення

p (n) S1 (n) if B (n) then p (n - 1) S2 (n)

4. Каскадна рекурсія

p (n) S (n) if B1 (n) then p (n - 1) if B2 (n) then p (n - 1)

Ця рекурсія називається каскадної, тому що кожен виклик підпрограми може породжувати кілька рекурсивних викликів (каскад).

5. Дистанційна рекурсія:

f (i: integer): integer; begin if B1 (n) then Result: = ... else Result: = f (f (i-1)); end;

Прикладом віддаленої рекурсії служить функція Аккермана :

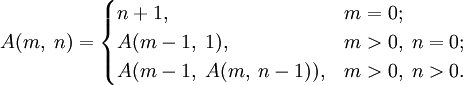
Приклади поганого і хорошого використання рекурсії

Приклад поганого використання рекурсії - числа Фібоначчі

Числа Фібоначчі задаються наступним рекурентним співвідношенням:

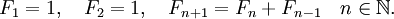
Ми вже обчислювали їх за допомогою циклів. Можливо рекурсивне (погане!) Рішення:

function Fib (n: integer): integer; begin if (n = 1) or (n = 2) then Result: = 1 else Result: = Fib (n - 1) + Fib (n - 2); end;

Ось що станеться при виклику Fib (7):

дерево рекурсивних викликів

Як бачимо, одні і ті ж числа обчислюються по кілька разів:

• Fib (7): 1
• Fib (6): 1
• Fib (5): 2
• Fib (4): 3
• Fib (3): 5
• Fib (2): 8

Алгоритм можна поліпшити, використавши масив, спочатку заповнений нулями.
При першому обчисленні fib (n) будемо заповнювати відповідний елемент, а при всіх наступних - просто звертатися до його значенню. Подібна методика називається мемоізаціей , Тобто запам'ятовуванням проміжних результатів для виключення їх повторного обчислення.

var F: array [1..1000] of integer; function Fib (n: integer): integer; begin if F [n] <> 0 then Result: = F [n] else if (n = 1) or (n = 2) then begin Result: = 1; F [n]: = 1; end else begin Result: = Fib (n - 1) + Fib (n - 2); F [n]: = Result; end; end;

Очевидно, даний спосіб вкрай неефективний в порівнянні з ітераційним алгоритмом як по пам'яті, так і за часом роботи. Зокрема, глибина рекурсії при обчисленні n-того числа Фібоначчі становить n-1.

Рекурсивний спосіб обчислення чисел Фібоначчі, побудований за ітераційного алгоритму

Нагадаємо ітераційний алгоритм пошуку n-того числа Фібоначчі:

a: = 1; b: = 1; for var i: = 3 to n do begin c: = a + b; a: = b; b: = c; end; Result: = c;

Побудуємо за нього рекурсивний алгоритм, передаючи в кожну рекурсивную підпрограму змінні a, b, c, мінливі на кожній ітерації циклу. Фактично при кожному рекурсивном виклик ми будемо здійснювати підстановку:

(A, b) -> (b, a + b)

Рекурсивний алгоритм, реалізований за цією підстановці, матиме вигляд:

function fib (a, b, n: integer): integer; begin if n = 1 then Result: = a else Result: = fib (b, a + b, n - 1) end; begin for var i: = 1 to 10 do Print (fib (1, 1, i)); end.

Рекурсія в даному прикладі - кінцева. Як уже зазначалося, вона легко замінюється итерацией, при цьому як раз виходить попереднє ітераційне рішення. Хороші оптимізують компілятори роблять це автоматично.

Приклад хорошого використання рекурсії - ханойські вежі

Завдання полягає в наступному:
Дано три стрижня. На першому лежать n дисків різного радіусу за умови, що жоден диск більшого радіусу не лежить на диску менше радіуса.
Hеобходимо перенести диски з першого стрижня на третій, користуючись другим, за умови:

• за один хід можна переносити тільки один диск
• менший диск повинен лежати на більшій

Ідея алгоритму така:

перекладаємо n-1 диск з вихідного стрижня на допоміжний залишився диск перекладаємо на необхідний стрижень лежать на допоміжному стрижні диски перекладаємо на необхідний диск

Т.ч. маємо просте рекурсивне рішення:

procedure MovePiramid (n: integer; f, t, w: integer); begin if n = 0 then exit; MovePiramid (n - 1, f, w, t); writelnFormat ( 'Перекласти диск з {0} на {1}', f, t); MovePiramid (n - 1, w, t, f); end;

Швидке сортування

алгоритм

Алгоритм швидкого сортування (різновид алгоритму «розділяй і влавствуй») складається з двох етапів:
1. Вибір деякого елемента масиву x і поділ масиву на дві частини так, що в першій виявляються всі елементи <= x, а в про другий -> = x
2. Рекурсивне застосування нашого алгоритму до отриманих частин

Очевидно, алгоритм буде працювати тим швидше, чим на більш рівні частини ми будемо ділити масив (в ідеалі - кожен раз навпіл).
Тому ми повинні прагнути вибрати елемент x так, щоб приблизно половина елементів масиву була <= його, і, відповідно, друга половина -> =. З іншого боку, вибір x не повинен займати багато часу і, по крайней мере, не залежати від n - розміру масиву).

Ми будемо використовувати найпростіший спосіб вибору x - як нього брати перший елемент.

Наступного анімації представлений приклад застосування алгоритму швидкого сортування до масиву

4 1 7 3 2 9 5 8 6

Розглянемо етап 1 докладніше:
- Для поділу масиву на зазначені частини заведемо 2 індексу i і j.
- На початку i буде вказувати на перший елемент і рухатися вправо, а j - на останній і рухатися вліво.

Крок 1.
Будемо просувати i вперед до тих пір, поки A [i] не стане> = x.
Далі будемо просувати j назад до тих пір, поки A [j] не стане <= x.
Прийшли до елементів A [i] і A [j], які "стоять не на своїх місцях" (згадаємо, що ми хочемо розкидати все менші або рівні x елементи вліво, а великі або рівні - вправо)
Крок 2.
Поміняємо їх місцями і просунемо i вперед на один елемент, а j - тому, також на один елемент.

Будемо повторювати зазначені дії до тих пір, поки i не стане> = j.
В результаті отримаємо масив A, розділений на 2 частини:

• зліва все елементи <= x
• праворуч -> = x

код програми

// Швидке сортування Ч. Хоара /// Поділ a [l] .. a [r] на частини a [l] .. a [q] <= a [q + 1] .. a [r] function Partition ( a: array of integer; l, r: integer): integer; begin var i: = l - 1; var j: = r + 1; var x: = a [l]; while True do begin repeat Inc (i); until a [i]> = x; repeat Dec (j); until a [j] <= x; if i <j then Swap (a [i], a [j]) else begin Result: = j; exit; end; end; end; /// Сортування частин procedure QuickSort (a: array of integer; l, r: integer); begin if l> = r then exit; var j: = Partition (a, l, r); QuickSort (a, l, j); QuickSort (a, j + 1, r); end; const n = 20; begin var a: = ArrRandom (); writeln ( 'До сортування:'); Writeln (a); QuickSort (a, 0, a. Length - 1); writeln ( 'Після сортування:'); Writeln (a); end.

Асимптотична оцінка складності

Будемо виходити з того, що масив щоразу ділиться на 2 однакові частини. Це найкращий варіант.
Глибина рекурсії в цьому випадку = log2n.

Очевидно, що в алгоритмі Partition ми переглядаємо всі елементи «своєї частини» рівно один раз. Тобто на кожному рівні рекурсії будуть по одному разу переглянуті всі елементи масиву.
Це означає, що асимптотична складність Partition на кожному рівні рекурсії = Θ (n).

Т.ч., за умови поділу приблизно навпіл, асимптотична складність всього алгоритму = Θ (n log n).

Теоретично доведено, що в середньому, якщо ділимо неточно навпіл, асимптотична складність зберігає формулу Θ (n log n).
Питання: яка складність в гіршому випадку? Найгірший - коли в якості x вибираємо мінімальний (або максимальний) елемент. Це відбувається (в нашій ситуації, тому що ми вибираємо перший елемент), якщо масив вже відсортований.
В цьому випадку в результаті розбиття на частини більша частина буде зменшуватися на 1, і глибина рекурсії в процедурі Sort буде дорівнює .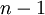
Тому в гіршому випадку асимптотична складність = .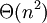

Затвердження. Для довільних даних не існує алгоритму з асимптотической складністю краще, ніж Θ (n log n) в середньому.

Генерація всіх перестановок

Основна ідея алгоритму генерації всіх перестановок полягає в наступному. У масиві довжини n, що містить перестановку, будемо міняти останній елемент з кожним, після чого будемо рекурсивно будемо робити те ж саме для масиву довжини n-1 і потім повертати переставлений елемент на старе місце. Якщо досягнута довжина масиву n = 1, то переставляти нічого не потрібно, а слід видавати вміст всього масиву-перестановки на екран. Такий алгоритм дозволить згенерувати всі перестановки, що випливає з словесного рекурсивного визначення: на останньому місці побуває кожен елемент, що міститься в даному масиві, після чого до решти масиву рекурсивно буде застосований той же алгоритм.

procedure Perm (a: array of integer; n: integer); begin if n = 1 then Writeln (a) else for var i: = 0 to n - 1 do begin Swap (a [i], a [n - 1]); Perm (a, n - 1); Swap (a [i], a [n - 1]); end; end; const n = 3; begin var a: = ArrGen (n, i -> i, 1); Perm (a, n); end.

Неважко бачити, що глибина рекурсії становить n-1, а кількість викликів процедури Perm становить n !.

Генерація всіх підмножин

Генерація всіх підмножин є алгоритм перебору. В алгоритмах перебору перебираються всі варіанти і для відповідних варіантів виконується певна дія. В даному випадку просто виводяться всі підмножини.

procedure Generate (A: array of integer; i: integer; Subset: LinkedList <integer>); begin if i = A. Length then Subset. Println else begin Generate (A, i + 1, Subset); // не додавати Subset. AddLast (A [i]); Generate (A, i + 1, Subset); // додати Subset. RemoveLast; end; end; begin var A: = Arr (5, 3, 8, 13, 15); var Subset: = new LinkedList <integer>; Generate (A, 0, Subset); end.

Перебір з поверненням (backtracking)

Загальна схема перебору з поверненням

procedure backtracking (k: integer); // k - номер ходу begin {запис варіанту} if {рішення знайдено} then {висновок рішення} else {перебір всіх варіантів} if {варіант підходить} then backtracking (k + 1); {Стирання варіанту} end; begin backtracking (1); end.

Питання про обході конем шахової дошки

const n = 8; var dx: = Arr (2, 2, 1, 1, - 1, - 1, - 2, - 2); dy: = Arr (1, - 1, 2, - 2, 2, - 2, 1, - 1); type KnightProblem = class Solution: = new integer [n, n]; Success: boolean: = false; procedure Step (i, x, y: integer); begin if Success then exit; // відсікання невірних варіантів if (x <0) or (x> = n) or (y <0) or (y> = n) or (Solution [x, y]> 0) then exit; // запис часткового вирішення Solution [x, y]: = i; if i = n * n then Success: = true else for var k: = 0 to 7 do // перебір варіантів Step (i + 1, x + dx [k], y + dy [k]); if not Success then Solution [x, y]: = 0; // повернення - стирання часткового вирішення end; end; const x0 = 1; // початкова клітина коня y0 = 3; begin var kp: = new KnightProblem (); kp. Step (1, x0, y0); if kp. Success then writeln (kp. Solution); writelnFormat ( 'Час: {0} мс', Milliseconds / 1000); end.